Priority
Prioritizing trees for harvest is a matter of designing a function that can quantitatively evaluate the relative value of one tree over another. Trees are always cut in order of highest to lowest cut priority, subject to stand-level tree retention constraints and spatial crop tree spacing limitations and selection error. If cut priority is not set, then the tree sort is random.
· Crop tree spacing (BINS command)
· Introducing random disorder (DISORDER command)
Preparing for Tree Sorting
Tree record partitioning
In cases where the tree list contains many trees, but very few tree records, sort randomization will be limited. For example, a tree list with 500 spruce and 500 fir in two tree records could only have two possible sort orders and it is likely that a random cutting will generate extreme selection bias toward either spruce or fir. While this is an extreme example, it illustrates the need for a more robust sorting approach.
To solve this problem, if trees per hectare in a tree record are greater than 1, OSM will temporarily partition the tree record into X parts so no more than 1 tree is present in any one record. This approach adds operational realism by allowing more effective sorting and randomization of individual trees, rather than tree records. It also makes it possible to randomly distribute individual trees into crop tree selection spaces.
Randomization
After partitioning, but before prioritization begins, tree records are randomly sorted. Therefore, if no priority rules are stated, random tree cutting will occur, subject to tree retention constraints. Where no priority rule is stated, or priority ties exist, it is likely that you will see slight cut choice differences between successive simulations because of this randomization. To ensure successive runs produce exactly the same results, see command SIMULATION.MODEL.SetRandomSeed.
Building Priority Rules
The PRIORITY command allows certain tree attributes (e.g., species, tree size, competitive status, growth increment, grade, and/or risk of mortality) to influence sorting of trees from highest to lowest cut priority. OSM tree attributes that can be incorporated into sorting rules are listed in the table below.
|
Tree Variable |
Metric |
Data Type |
Description |
|
DBH |
cm |
Double |
Diameter at breast height outside bark |
|
DBHI* |
cm/yr |
Double |
DBH increment projected by model |
|
HT |
M |
Double |
Height to tip of leader |
|
HTI* |
m/yr |
Double |
Height increment projected by model |
|
BAL |
m2/ha |
Double |
Basal area of larger trees |
|
CR |
ratio |
Double |
Ratio of live crown length to total tree height |
|
MR* |
ratio/yr |
Double |
Probability of tree mortality this year predicted by model |
|
- |
Byte |
Classification user or Variant defined. |
|
|
RiskϮ |
- |
Byte |
Classification user or Variant defined. |
* Based on predictions from the previous simulation cycle, or in the case of cycle 0 based on field data. Unless these values exist in field data, these attributes should not be used to prioritize cutting in the first simulation cycle because none of these attributes will have prediction values assigned until simulation cycle 1.
Ϯ May not be predicted by the Variant model.
Simple priority rule
To thin trees from below, small DBH trees need to be assigned a higher cut priority value than large trees. This can be accomplished using the following sort function:
![]()
Multiplying DBH by -1 reverses the sort direction so trees are sorted by smallest to largest DBH in the cut priority list, instead of largest to smallest. Larger priority values are always cut first.
To state this same rule in OSM commands, use:
def MyExampleAction
Priority
DBH -1
To thin from above, use: ![]()
Priority
DBH 1
If no cut priority commands are used, the tree list sort is random. In other words, crown or geometric DBH thinning is the default priority rule in OSM.
Complex priority rules
To first prioritize shortest trees, and then by poorest tree grade class (tree bole quality), the following may be stated:
Priority
HT -1000
Grade 1
These commands, once compiled, equate to:
![]()
, where HT is tree height and Grade is a user or Variant defined tree form or quality classification.
In this example, let’s assume a higher Grade class indicates lower quality (trees we want to cut first). By weighting height by -1000, we guarantee that shortest trees will always be cut first, regardless of tree Grade. Where height ties exist, trees with higher Grade class values (lower quality) will be cut first. In the case of tree Grade, larger class values are undesirable, so we multiply by 1, not -1.
Note that Grade and Risk classes in OSM can
range between 1 and 255, but depend on the user’s or
Variant’s own classification system; e.g., higher Grade classes may sometimes indicate
better quality. Grade and Risk class values are assigned in the tree list by users before the tree list is loaded to
OSM and/or are predicted. Consult Variant documentation on whether grade or
risk models have been declared.
To illustrate, consider the following tree list. Red values indicate undesirable trees (should be cut) relative to green, desirable values (should be retained if possible).
|
Tree ID |
HT (m) |
Grade |
|
1 |
5 |
1 |
|
2 |
5 |
4 |
|
3 |
14 |
6 |
|
4 |
20 |
1 |
|
5 |
25 |
1 |
|
6 |
6 |
4 |
|
7 |
2 |
3 |
|
8 |
30 |
3 |
|
9 |
16 |
7 |
|
10 |
18 |
8 |
By using:
![]()
, the tree list is sorted by highest to lowest cut priority, as shown below.
|
Tree ID |
HT (m) |
Grade |
Cut Priority
Result |
|
7 |
2 |
3 |
-1997 |
|
2 |
5 |
4 |
-4996 |
|
1 |
5 |
1 |
-4999 |
|
6 |
6 |
4 |
-5996 |
|
3 |
14 |
6 |
-13994 |
|
9 |
16 |
7 |
-15993 |
|
10 |
18 |
8 |
-17992 |
|
4 |
20 |
1 |
-19999 |
|
5 |
25 |
1 |
-24999 |
|
8 |
30 |
3 |
-29997 |
If we want less priority on height and slightly more on Grade, we could state:
![]()
, which would cause the tree list to be sorted as:
|
Tree ID |
HT (m) |
Grade |
Cut Priority
Result |
|
10 |
18 |
8 |
7 |
|
9 |
16 |
7 |
6 |
|
2 |
5 |
4 |
5.5 |
|
7 |
2 |
3 |
5 |
|
6 |
6 |
4 |
5 |
|
3 |
14 |
6 |
5 |
|
1 |
5 |
1 |
-0.5 |
|
4 |
20 |
1 |
-8 |
|
8 |
30 |
3 |
-9 |
|
5 |
25 |
1 |
-10.5 |
Note in the example above that the resulting cut priorities are not simply sorting by tree height and then by Grade or vice versa. Instead, this sort was designed to prioritize trees with poor Grade first, but only if differences in height are not too extreme. Grade classification systems will vary among jurisdictions, and class values may need to be redefined to make them applicable for building priority rules. This is merely an example of how one might incorporate tree attributes like Grade into a cut priority function.
Prioritizing by species
First, a new ranked set of species must be defined. This is done outside of the Actions section in using the SPECIES command.
MySpeciesCutPriority
RS -1000
WS -100
BS -100
BF 1000
Second, the name of the ranked set of species defined above must be referenced in the Priority function.
def MyExampleAction
Priority
MySpeciesCutPriority 1
The species/DBH sorting function above will cause balsam fir (BF) to be cut before spruce, and white (WS) and black spruce (BS) before red spruce (RS). Any trees not listed in the ranking definition will have a ranked value of zero. Balsam fir will be cut before any other species, and likewise, spruce will be retained before all other species. If only species rank values are used to control the sort, then trees having the same species rank value will be sorted randomly within each rank.
Complex cut priority rules can be designed using a combination of a species rank list and as many other tree attributes as desired. In the example below, because DBH -1 is also stated, once trees are sorted by species, trees with the same species rank will be sorted for cut by smallest DBH first. By putting some thought into the relative rank value of species and weights on both species and DBH, it is possible to trade-off species priority in favor of DBH priority where DBH differences are large.
Priority
MySpeciesCutPriority 1
DBH -1
Adding Spatial Limitations
Operationally, it is impossible to prioritize trees for harvest perfectly due to incomplete knowledge of all trees in the stand during harvest, non-uniform distribution of crop trees, and selection errors. Plantations, where crop trees are well spaced and easily identified may be easier to prioritize in the field compared to a species rich, uneven-aged stand with randomly distributed trees. Complexity of the prescription and operator experience may also hinder optimum selection of best crop trees for a given prescription; e.g., professional tree marker compared to an inexperienced harvest equipment operator.
To introduce some operational realism into the ‘ideal’ prioritized cut list, commands can be introduced to simulate 1) crop tree space and selection limitations (BINS command) and 2) crop tree omissions and selection errors (DISORDER command). Both commands can be used at the same time, but choosing one that might work best for your prescription and pre-treatment stand conditions is generally recommended. Discussion of use and examples of each command in the following sections should help you to decide which might be more appropriate to use for your simulations. Generally speaking, the BINS command works well in cases where randomly distributed crop trees are to be spaced (thinned) uniformly; e.g., pre-commercial thinning. Whereas, the DISORDER command may work better in cases where crop trees are already uniformly spaced in the pre-treatment stand condition (e.g., plantation cleaning or thinning), but random crop tree selection issues prevent flawless thinning. For complex treatments, like hardwood single-tree selection method, some combination of the two commands may be used to introduce some crop tree spacing limitations (BINS) and tree marking error (DISORDER).
Crop tree spacing (BINS command)
OSM tree records are not spatially explicit, nor do they represent individual trees; so, exact spatial modeling of crop tree selection is not possible. However, it is possible to randomly assign partitioned individual trees to explicit locations within the stand. Once tree spatial locations are assigned, trees can be spatially grouped into crop tree spaces (BINS) within the stand. Area of each crop tree space (BIN) is defined indirectly by the BINS command argument, which defines the number of crop trees spaces within a unit area. Prioritization and selection of crop trees can then be spatially limited to the scope of trees falling within each BIN.
BINS Argument = {number of crop trees per hectare – or acre if USA units used}
For example, consider a stand of 100 tree records representing 20,000 individual trees per hectare comprised of five species distributed randomly and in equal proportion throughout the stand. Assume we wish to perform a pre-commercial thinning on this stand to promote one of the five species and retention of only 2,000 crop trees per hectare. If we were to simply sort by species cut priority and retain 2,000 trees, the treatment would be 100% successful in retaining 2,000 trees of the desired species. However, assuming trees are randomly positioned, there are likely to be cases where the desired species is not present within a given crop tree space. There may even be cases where the space is void of any trees.
Adding the BINS command with 2,000 bins, as shown below, will cause the partitioned trees to be randomly allocated to one of 2000 bins. Trees are still sorted from lowest to highest cut priority, but sorting is restricted to each bin. The best tree in each bin (lowest cut priority, highest retention priority) is considered first for retention.
The retention command below states that ≥2,000 trees must be retained, and are, but with BINS those 2,000 trees will not all be the same species. With 2,000 BINS and 20,000 trees, there will be about an 86% chance that the desired species will be present in any given bin; assuming the desired species represents 20% of total trees. At 10k, 4k, 2k, or 1k initial trees, this same probability drops to roughly 64%, 32%, 18%, or 9%, respectively.
Actions
def
MyExampleAction
Cut
Priority
MySpeciesCutPriority 1
DBH -1
BINS 2000
Retention
Trees >= 2000
Note that the
BINS command does not control tree retention. BINS are only used to restrict
crop tree prioritization locally within the stand. Stating BINS 2000
will not retain 2000 trees without a retention statement to do so. For the
example above, at 20k, 10k, 4k, 2k, or 1k initial trees and 2,000 BINS, 0%,
0.7%, 13.6%, 28.5%, or 60.6% of BINS will not contain any trees, respectively;
yet 2000 trees will be still be retained in all but the last case.
If the retention constraint(s) is not satisfied after examining the first layer of priority crop trees, the second best crop tree from each bin is considered, and so on, until all trees have been considered for retention or the retention constraint is satisfied. In other words, OSM is permitted to select more than one crop tree per BIN in order to satisfy retention constraints, but only after examining all other BINS for a suitable crop tree first. This relaxation is important to avoid over stating the influence of spatial constraints. Ideally, it would be preferable to allow selection of 1 crop tree from each BIN; however, this requires complete knowledge of the spatial distribution (uniform, random, clumped) of trees in the stand, and for trees to be modeled as individuals. In reality, the spatial distribution of trees is unlikely to be purely random. Purely random distributions tend to result in many empty or low tree count BINS, which could lead to far fewer crop trees retained in the model than possible in practice. Also consider that tree markers and harvest operators can make minor spacing adjustments between bins (crop trees spaces) to move the average stand condition closer to stand-level retention targets.
Competition for resources (light, nutrients, and water) leads the stand toward more of a uniform distribution of trees than random. Because trees are allocated to BINS randomly, there may be a greater number of empty BINS simulated in OSM then actually exist in the stand. As the ratio of pre-treatment stand density to crop tree BINS is reduced, probability of empty BINS increases dramatically (Figure 1), which may or may not be realistic. Unless the stand to treat has an extremely random or clumped distribution of crop trees, BINS should be set 5 to 10 times lower than the pre-treatment density of the stand. When # of BINS equals number of pre-treatment trees, crop tree selection is completely random. As BINS approach 1, infinitely less disruption of the ‘ideal’ priority list occurs. In cases where the stand has an extremely uniform distribution of crop trees, as in a plantation, BINS should be >10 times less than pre-treatment densities; perhaps even 100 times less. For very uniform conditions, consider using the DISORDER command instead to introduce random crop tree spacing issues and/or crop tree selection errors.
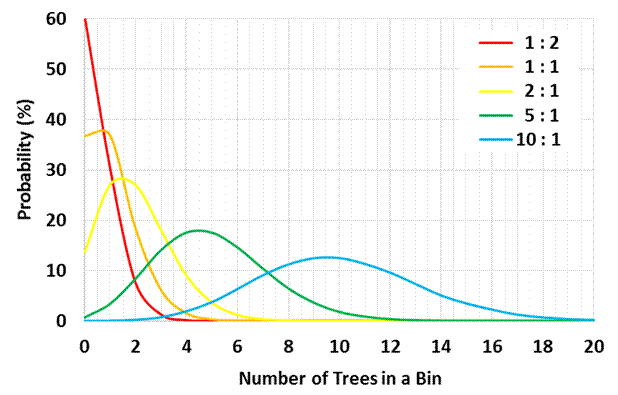
Figure 1. Frequency distribution of trees allocated to BINS for five stand density to BINS ratios.
Introducing random disorder (DISORDER command)
The cut priority DISORDER command can be used to introduce a degree of random disorder into the ideal ordered cut list. This command is useful when simulating random crop tree omissions (e.g., failed or ill spaced plantation crop trees) and/or occasional crop tree selection errors during harvest. By default, OSM will cut trees in the ideal cut priority order (DISORDER = 0%). If DISORDER is set >0%, to say 10% (see example below), then the random positions of 10% of sorted tree records will be swapped with the random positions of another 10% of trees in the list.
Actions
def
MyExampleAction
Cut
Priority
MySpeciesCutPriority 1
DBH -1
DISORDER 10%
Random swapping of prioritized trees is with replacement, so swapping 50% of trees with another 50% of randomly selected trees would rarely equate to 100% of trees randomly reordered (Fig. 2). If BINS are set > 1, then trees randomly falling within each bin are disordered using the same approach.
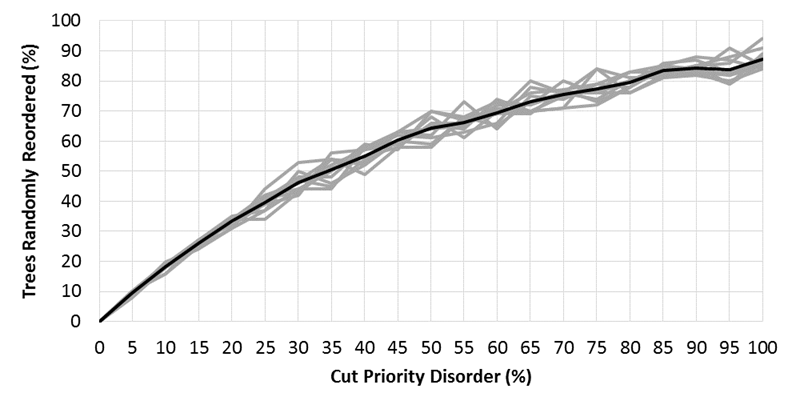
Figure 2. Percent of 100 trees that were reordered at cut priority disorder levels of 0-100% following for 10 repeated simulations (gray; average black)